したがって、モデルの対称性から計算領域は左下4分の1部分だけである。
(積分形式に基づく差分法なら、正確に4分の1で良い)
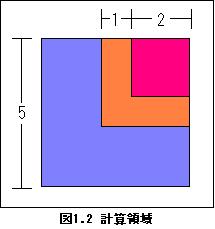 計算領域を図1.2に示す。
計算領域を図1.2に示す。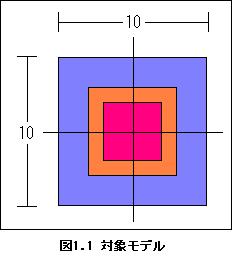
領域を差分法によって離散化して係数行列を作り、反復解法によって解く。
差分法は、積分形式に基づく差分法を用いる。
反復解法は、PCG法(前処理付き共役勾配法)を用いる。
<モデル>
モデルは2次元で与える。
対象とするモデルを図1.1に示す。
赤色の部分は、熱伝導係数 k=1.0[W/mK],発熱量 f=20.0[WK/m2] の物質である。
その周りの茶色の部分は断熱材として、k=0.01,f=0.0 を与える。
青色の部分は、k=1.0,f=0.0 の物質とする。
正方形状のモデルは上下左右対称で、境界条件はすべて第1種とする。
したがって、モデルの対称性から計算領域は左下4分の1部分だけである。
(積分形式に基づく差分法なら、正確に4分の1で良い)
 計算領域を図1.2に示す。
計算領域を図1.2に示す。
領域を100×100等分し、差分法で離散化する。
5点差分を反復解法で解く場合、係数行列に必要なメモリ量は、
およそ100×100×3=30,000ダブルワード=約240Kバイト程度で済む。
参考のために、直接解法の例を挙げると、
通常のガウス消去法ならば、100×100×100×100=100,000,000ダブルワード=約800Mバイト必要である。
対称帯ガウスならば、100×100×100=1,000,000ダブルワード=8Mバイトほどである。
さらに、モデルを3次元にした場合には、直接解法ではメモリ量だけを見ても、限界であることが分かるであろう。
パソコンを使って、離散化してできた連立方程式をPCG法で解いたところ、
ICCG(1,1)法では、反復回数115回で約1.6秒、
MICCG(1,1)法では、反復回数58回で約0.7秒であった。(共に収束判定の精度は、小数点以下10進8桁)
使用したパソコンは、「FortranとC言語の比較1」で使用したものと同じもので、Fortranのみで行った。
<結果>
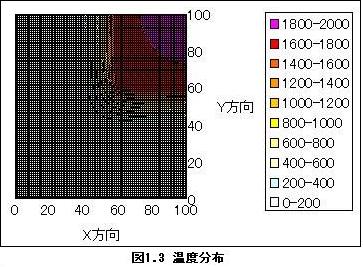 計算結果を図1.3に示す。
計算結果を図1.3に示す。
図の右上、つまりモデルの中心が当然のごとく一番高温となっていて、断熱材の領域から温度は一気に下降していることが分かる。
冷却装置を取り付けたり、断熱材の材質を変えることによって、周囲の温度上昇を防いだりするなど実際の問題にも応用できると考える。
計算時間などは上記のとおりである。
SOR法やCG法でも行ったが、SOR法では収束するまでに非常に時間がかかった。
参考のために述べておくと、
CG法では、反復回数1395回で約11秒、
SOR法では、加速係数をYoung-Frankelの理論より算出し、精度を10進4桁にしても反復回数が10000回を越え、計算時間も50秒以上になったので打ち切った。