有限要素法による非定常熱伝導問題のシミュレーション
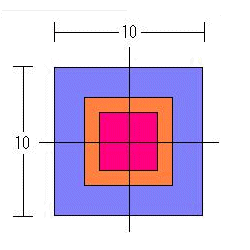
<物理モデル> 図1の熱伝導問題
(差分法におけるPCG法を用いたシミュレーションと同じモデル)
図1 対象モデル
赤色の部分は、熱伝導係数 k=1.0[W/mK],発熱量 f=10.0[WK/m3] の物質である。
その周りの茶色の部分は断熱材として、k=0.01[W/mK],f=0.0[WK/m3] を与える。
青色の部分は、k=1.0[W/mK],f=0.0[WK/m3] の物質とする。
領域Ω内の物質の熱容量はすべてρ=1.0[J/m3K] とした。
正方形状のモデルは上下左右対称で、境界条件はすべて第1種である。
<目的>
時間依存問題のシミュレーション
<方法>
- 離散化:有限要素法(三角形1次要素)
- 時間依存部分の処理:クランク−ニコルソン法による時間差分
- ソルバ:CG(Conjugate Gradient)法
<計算環境>
- CPU : Intel Celeron 566MHz
- メインメモリ : 128Mバイト
- コンパイラ : MS-VC++ 5.0
<モデルの詳細>
モデルの対称性から計算領域は右上4分の1部分だけで良い。計算領域を図2に示す。
図2 計算領域
モデルは以下の拡散方程式で表現できる。
- ρ・∂u/∂t + div{-k・grad(u)} = f in Ω
- u = 0 on Γ1
- {-k・grad(u)}×n = 0 on Γ2
節点数が400となるように領域を有限要素法で離散化する。これを反復解法で解く場合、係数行列に必要なメモリ量は、およそ 400×6 = 2,400ダブルワード = 約20Kバイト程度である。また、0秒(初期時刻)から20秒まで時間の刻み幅を0.1秒としたので、200回の時間反復を行った。
<シミュレーション結果>
図3に実験結果を示す。
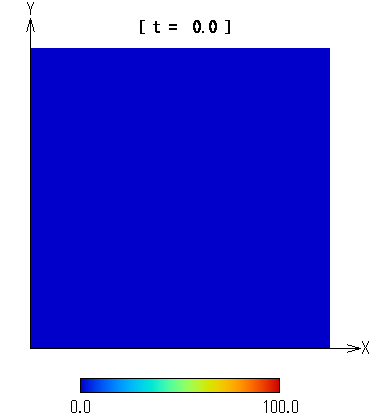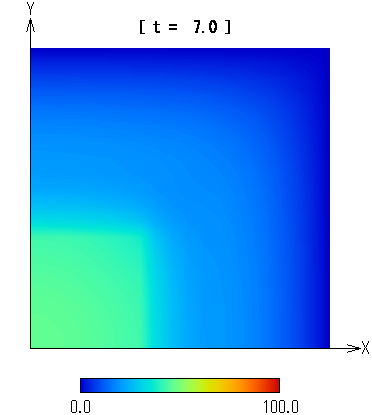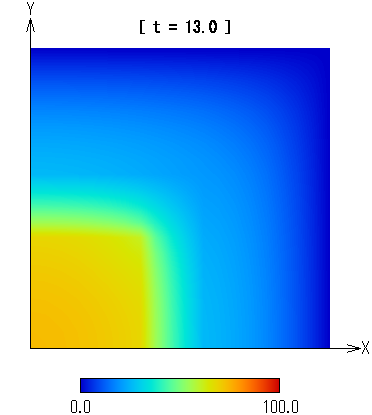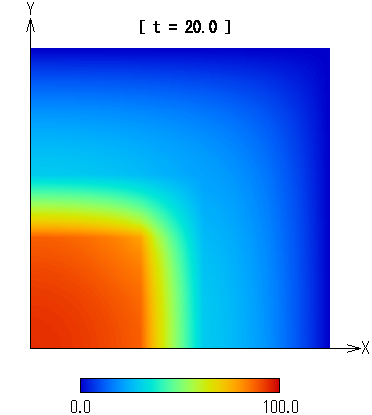
図3 熱伝導のシミュレーション画像
実験結果は1秒以内に得られた。
<コメントなど>
このモデルは、見ての通り特に有限要素法を使う必要もなく、差分法で素直に解けますが、現在手伝っている大学の学部ゼミにおいて色々作成する機会があったので、せっかくだからやってみようと思った次第です。
<グラフィックソフトについて>
結果の可視化のために、以下の画像処理ソフトを使用しました。
- ペイント (Windows98標準付属)
- AV似非(えーぶい・えせ) Ver.0.71 (フリーソフト)
- Animation GIF Maker Ver.0.71 (フリーソフト)
どうでも良いことですが、上記フリーソフトはどちらもバージョンが同じです。
Go back