本研究課題の目的は、ポスト「京」において、精度が保証された計算結果を実用的に得られるような超高性能計算環境を構築することです。具体的には、ポスト「京」で実行される様々な数値シミュレーションにおいて、数値計算による計算誤差の問題が解消されることによって、シミュレーションサイエンスの品質を向上させ、さらに想定外の現象が発生する可能性を低減することが可能となります。すなわち、本研究課題の遂行は、人が安心して生活できる社会基盤の構築に直結します。
たとえば、産業界における製品開発や非破壊検査等のための計算工学シミュレーションや、地震や津波などの災害シミュレーションは、日本に限らず世界中で盛んに行われていますが、計算誤差の観点から高精度なシミュレーションの実現をしている例は皆無です。これは、計算機によって問題の近似的な解を得ることよりも、その近似解の検算のほうがはるかに困難かつ計算資源を必要とする、と考えられており、それが高性能計算分野の常識であるからです。実際、これは1990年代までは事実でしたが、本研究グループが2000年代から切り拓いてきた高速で実用的な精度保証付き数値計算法やエラーフリー変換に基づく高精度数値計算法をベースとして、今、ポスト「京」によって、この常識を打ち破る時期が到来しています。すなわち、ポスト「京」において、高速性と高精度性を融合した超高性能計算環境の創成を世界に先駆けて達成することは、スーパーコンピュータに質的転換をもたらし、我が国の高い科学技術力を国内外に示すことになります。
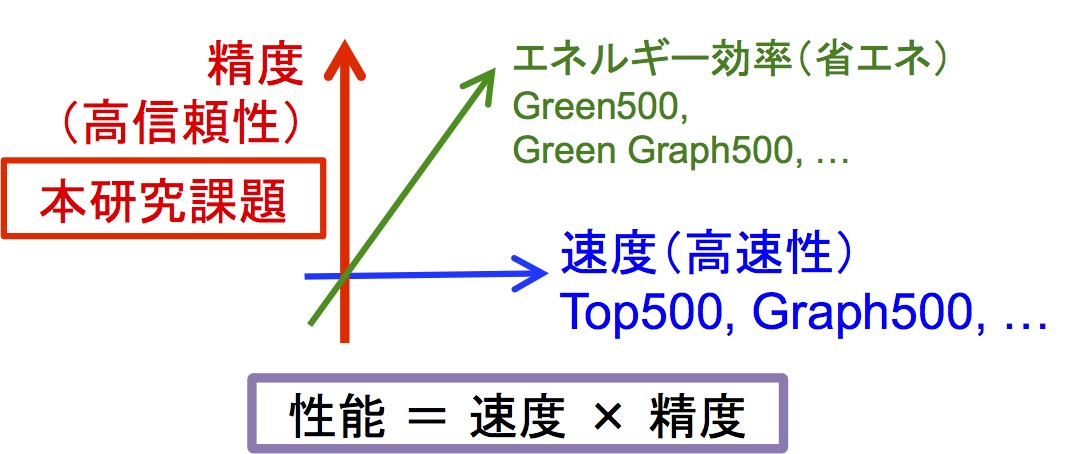
大規模数値計算を行う高性能計算分野においては、問題の大規模化に伴って計算誤差が累積しやすくなり、これが今後、大きな問題となってきます。たとえば、計算機上で標準的に用いられる32ビットの浮動小数点演算では、100万次元程度の密行列系線形問題に対して数値計算を行うと、問題自身は比較的良条件で解きやすい問題であったとしても、誤差解析の結果から理論的には1桁も正しくないような計算結果が得られることが分かっています。また、計算誤差の単なる累積だけでなく、問題の困難さが条件数として行列に反映されるため、問題自身が悪条件であれば、より小規模の問題においても意味のある解を得られなくなります。このように、計算処理の高速性のみを追求するような高性能計算の方針は、既に限界を迎えつつあります。
このような状況において、本研究課題によって提案するような「精度」の軸が導入された超高性能計算環境は、現在、世界のどこにも存在しないものですので、この実現は極めてインパクトが高く、「世界に前例のない高速性を持つスーパーコンピュータ」と「世界をリードしている高精度性を持つ数値計算法」の融合を目的とする本研究課題の成果が、高性能計算分野及び精度保証付き数値計算分野において世界をリードするものとなることは明らかです。
さらに、このような超高性能計算環境をベースとして、基礎科学における計算誤差に起因した各種の難問に本研究成果が応用されることによって、世界初の研究成果が創出されることが期待されます。
